

Fast Construction of Accurate Quaternion SplinesRavi Ramamoorthi Computer Graphics Laboratory California Institute of Technology | |
Abstract
In 1992, Barr et al proposed a method for interpolating
orientations with unit quaternion curves by minimizing covariant
acceleration. This paper presents a simple
improved method which uses cubic basis functions to achieve a speedup
of up to three orders of magnitude. A new criterion for automatic
refinement based on the Euler-Lagrange error functional is also introduced.
SummarySplines have been widely used to interpolate keyframe translations and are generally based on rigid variational principles. For instance, the cubic spline minimizes the integral of the square of flat-space acceleration. Because of the curvature of rotational space, it has not been possible to find an analog to flat-space splines. Curves with simple analytic forms are not variationally optimal, and analytic formulae for "minimal" curves are not known. By using unconstrained minimization and cubic splines as basis functions, we speed up previous work in numerically constructing variationally optimal quaternion curves, thus allowing minimization of covariant acceleration to be used as an interactive tool. In the process, we introduce a new method for rapid adaptive refinement of an approximate solution based on the error as measured by the Euler-Lagrange error functional. Although we have dealt with construction of optimal rotational curves for animation, our methods are easily extensible to more general and complex motions. Further, splining in curved spaces and constructing optimal paths is of importance to a number of communities besides graphics, such as CAGD, robotics and kinematics. AlgorithmOur algorithm is simple to implement and is summarized as follows:
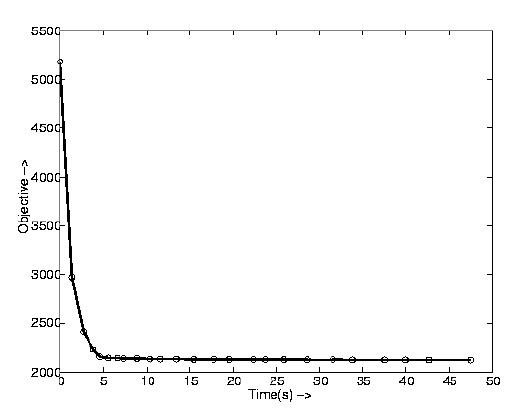
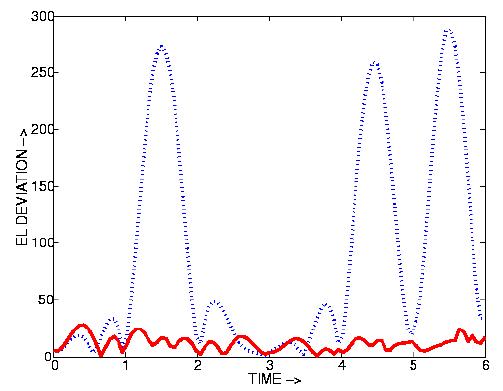
ResultsBesides the quaternion path shown in Figure 1, further results are shown in Figures 2,3 and 4. Clicking on each figure will bring up an enlarged version.Figure 2 Performance of the algorithm. The objective functional is plotted against wallclock time in seconds with each circle on the graph representing a higher level of optimization or addition of more variable frames. The results shown here are up to three orders of magnitude faster than previous work. Figure 3 Maintaining unit magnitude. In the original path (blue dotted), there are significant deviations, while increasing levels of optimization (magenta dashdot and red solid line) bring the quaternions very close to unit magnitude. Figure 4 The blue dotted graph shows the initial Euler-Lagrange error. The solid red graph shows how this error is significantly decreased upon optimization. Relevant Links
|

|
| Figure 1. The interpolation problem in quaternion space, showing keyframes (large circles), variable frames (small circles), the optimized path (solid line) and the jerky unoptimized path (thin line). | |
| |
| Figure 2. Performance of the algorithm | |

| |
| Figure 3. Maintaining unit magnitude | |
| |
| Figure 4. Euler-Lagrange error | |
| Home | Research | Outreach | Televideo | Admin | Education |