

Correction of Geometric Perceptual Distortions in PicturesDenis Zorin Computer Graphics Laboratory California Institute of Technology | ||
AbstractWe suggest an approach for correcting several types of perceived geometric distortions in computer-generated and photographic images. The approach is based on a mathematical formalization of desirable properties of pictures. From a small set of simple assumptions we obtain perceptually preferable viewing transformations and show that these transformations can be decomposed into a perspective or parallel projection followed by a planar transformation. The decomposition is easily implemented and provides a convenient framework for further analysis of the image mapping. We prove that two perceptually important properties are incompatible and cannot be satisfied simultaneously. It is impossible to construct a viewing transformation such that the images of all lines are straight and the images of all spheres are exact circles. Perceptually preferable tradeoffs between these two types of distortions can depend on the content of the picture. We construct parametric families of transformations with parameters representing the relative importance of the perceptual characteristics. By adjusting the settings of the parameters we can minimize the overall distortion of the picture.
It turns out that a
simple family of transformations produces results that are
sufficiently close to optimal. We implement the proposed
transformations and apply them to computer-generated
and photographic perspective projection images.
Our transformations can
considerably reduce distortion in wide-angle motion pictures and computer-generated
animations.
SummaryThe process of realistic image synthesis can be subdivided into two stages: modeling the physics of light propagation in three-dimensional environments and projecting the geometry of three-dimensional space into the picture plane (the "viewing transformation.") While the first stage is relatively independent of our understanding of visual perception, the viewing transformations are based on the fact that we are able to perceive two-dimensional patterns - pictures - as reasonably accurate representations of three-dimensional objects. We can evaluate the quality of modeling the propagation of light objectively, by comparing calculated photometric values with experimental measurements. For viewing transformations the quality is much more subjective. The perspective projection is the viewing transformation that has been primarily used for producing realistic images, in art, photography and in computer graphics. One motivation for using perspective projection in computer graphics is the idea of photorealism: since photographic images have one of the highest degrees of realism that we can achieve, perhaps realistic rendering should model the photographic process. But the intuitive concept of realism in many cases differs from photorealism: photographic images, are often perceived as distorted (note the shape of the sphere in the photo from M. Pirenne's book. On the other hand, some paintings, while using perspective projection, contain considerable deviations from it. These paintings, however, are perceptually correct and realistic. In this paper we derive viewing transformations from some basic principles of perception of pictures rather than by modeling a particular physical process of picture generation. Our approach is based on formalizations of desirable perceptual properties of pictures as mathematical restrictions on viewing transformations. The main result allows us to construct usable families of transformations; it is a decomposition theorem which states that under some assumptions, any perceptually acceptable picture-independent viewing transformation can be decomposed into a perspective or parallel projection and a two-dimensional transformation. Our approach allows us to achieve several goals:
The transformations that we propose may have a number of applications: creation of computer-generated wide-angle pictures and wide-angle animations with reduced distortion, and correction of photographic images and movies. |
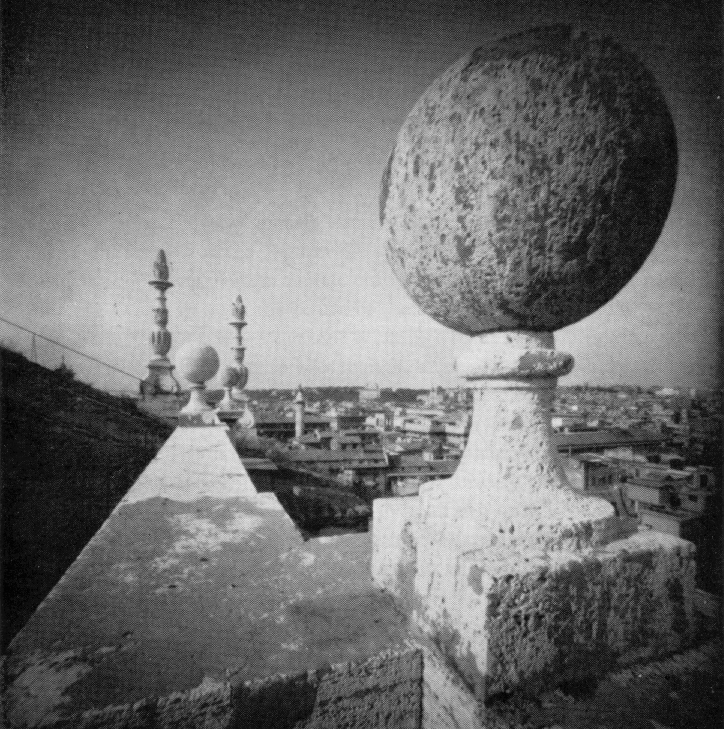
|

|
|
Left: Wide-angle pinhole photograph taken on the roof of the Church of
St. Ignatzio in Rome, classical example of perspective distortions from
the book M. Pirenne "Optics, painting and photography." ; reprinted with
the permission of Cambridge University Press.
Right: Corrected version of the picture with transformation applied. | ||

| ||

| ||

| ||
|
A wide-angle photograph of a room. Top: Original image (approximately 100 degrees field of view) Middle: Correcting transformation applied with maximal correction for shape distortion everywhere. Bottom: Correcting transformation applied, maximal correction of distortion of shape on the left, decreasing to the right across the image. Note the correct shape of the head and straightness of the walls. | ||

|

| |
| Details of the original and corrected photographs. | ||
| Home | Research | Outreach | Televideo | Admin | Education |